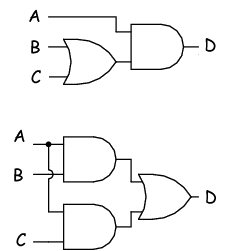
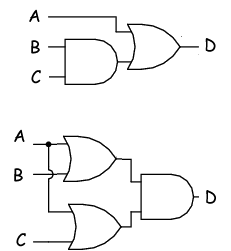
Distribution

I think of this as expanding the brackets! The distributive property allows us to expand a Boolean expression formed by the product of a sum, and in reverse shows us how terms may be factored out of Boolean 'sums-of-products':

This is (for my way of thinking as a physicist) best thought of in terms of logic gates.

( + ) = . + . =

Here we have and as inputs into an OR gate ANDed with . For the output to be high must be high and so must or .

If we do a truth table for this combination we find that the output is the same as that for and as inputs into an AND gate and the output of that gate then being ORed with the output of an AND gate with inputs and .

This is exactly like the usual algebaic expansion of brackets that you did in your first year at secondary school. Simples!

+ . = ( + ).( + ) =

Here we have and as inputs into an AND gate ORed with .

If we do a truth table for this combination we find that the output is the same as that for and as inputs into an OR gate and the output of that gate then being ANDed with the output of an OR gate with inputs and .

This is nothing like the usual algebaic expansion of brackets that you did in your first year at secondary school... but it is a case of swapping AND for OR and vice versa of the first expression. Simples!

When learning to use these expressions at college I always had to write them out at the start of an examination - make myself an equation sheet - in those days we were not given such things!!

For distribution I learned to write out the first of these expressions and then from that write out the second (sawapping AND for OR).