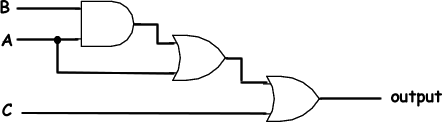Custom Search

Boolean Algebra

Boolean algebra (or Boolean logic) is a logical calculus of truth values.

It was developed by George Boole in the 1840s and took its name from him.

It resembles the algebra of real numbers.

numeric operation logical operation logic gates (electronics)
multiplication xy conjunction x∧y AND gate A.B
addition x + y disjunction x∨y OR gate A+B
negation −x negation ¬x NOT gate  

Simplification of Boolean expressions

This can be done by using the Laws of Boolean algebra. It is often used to simplify a logic circuit - minimising the number of components. This reduces the cost, risk of poor electrical connections and time of operation for the circuit.

Example

Simplify the circuit below.

The first step is to put the circuit into a Boolean expression. Let us call the output 'Y'. Then

Y = ((A.B) +A) + C

If we look at the ((A.B) + A) part of the equation we see that we can take the A outside the bracket and rewrite it as:

Consider: (A.B) + A = A((1.B) + 1)

As ((1.B) + 1) = 1 (identities)

we now have A.1 = A (Laws of 1s and 0s)

That gives us A.A = A (idempotent law)

We can therefore write:

Y = A + C and redraw the circuit as:

To check we are correct we can do a truth table:

A
B
C
A.B
A.B + A
(A.B + A) + C
A+C
0
0
0
0
0
0
0
0
0
1
0
0
1
1
0
1
0
0
0
0
0
1
0
0
0
1
1
1
1
1
0
1
1
1
1
1
0
1
0
1
1
1
0
1
1
0
0
1
1
1
1
1
1
1
1
1

It looks more complicated than it really is with all of that explanation written in!

Let us rewite it as simple Boolean Algebra simplification - the way you would do it in an exam situation:

Y = ((A.B) +A) + C

Y = A(B + 1) + C

Y = A(1) + C

Y = A + C

See Canonical Forms for how to extract a Boolean expression from a truth table.