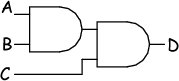
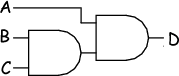
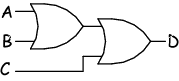
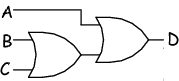Associativity

This is (for my way of thinking as a physicist) best thought of in terms of logic gates.

Associativity concerns the association (joining) of terms. When combining terms it turns out that the order in which they combine (either ANDed or ORed together) doesn't matter.

(.) = (.) =

Here we have and as inputs into an AND gate. The output of that gate then forms one input into a further AND gate - the other input being .

If we do a truth table for this combination we find that the output is the same as that for and as inputs into an AND gate and the output of that gate then forming one input into a further AND gate - the other input being .

The brackets are just there to show which two are associated together in the first gate. The outcome is unaffected by that choice as all three inputs have to be high for a high output.

In other words the brackets do not matter - we could write it as .. or .. or .. etc.

( + ) + = + ( + ) =

Here we have and as inputs into an OR gate. The output of that gate then forms one input into a further OR gate - the other input being .

If we do a truth table for this combination we find that the output is the same as that for and as inputs into an OR gate and the output of that gate then forming one input into a further OR gate - the other input being .

The brackets are just there to show which two are associated together in the first gate. The outcome is unaffected by that choice as any input being high produces a high output.

In other words the brackets do not matter - we could write it as + + or + + or + + etc.