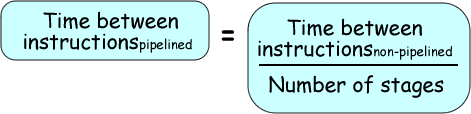
Pipelining: SpeedupIn parallel computing (using processors in a parallel arrangement), speedup refers to how much a parallel algorithm is faster than a corresponding sequential algorithm. When pipeling, speedup refers to how much a pipelined system is faster than a corresponding sequential one. If all stages are balanced i.e., all take the same time.
If the stages are not balanced, speedup is less, as you need to use the maximum time for an instruction. Speedup is due to increased throughput Speedup has no effect on latency (time for each instrucPon) does not decrease The potential maximum speed up occurs when all of the stages are done in parallel. This is impossible because it takes time for the instructions to get into the pipeline and then to fully leave it. Potential speedup = Number pipe stages Time to "fill" pipeline and time to "drain" it reduces speedup. Example:
The potential speedup would be four times (4X) - as there will be 4 tasks in the pipeline. But that would not be possible from the beginning, because one load would have to start while the other three waited in turn... we would only have the four 'on the go' after an initial time period. The 'pipeline' would only be fully operational then all four loads were being laundered. Then as soon as one was completed the pipeline would again not be 'full' so there would be a 'draining' period for the pipeline. The 'fill' and 'drain' stages affect the efficiency of the system. The speedup = sequential time/actual time = 8h/3.5h = X2.3
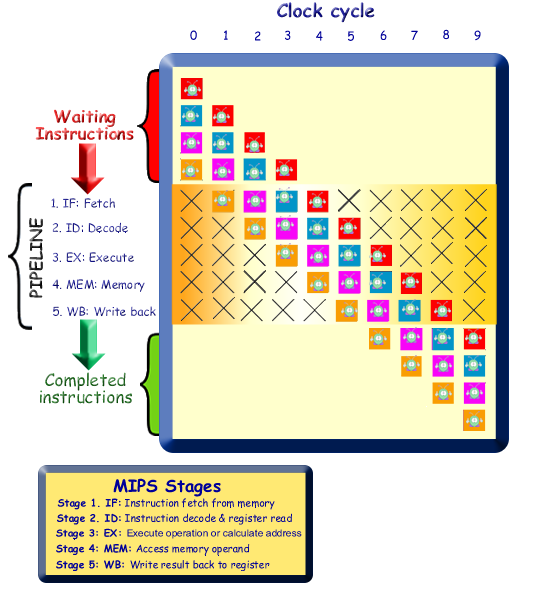
In the above example it takes 5 clock cycles to complete 1 load. Therefore sequentially it would take 5 x 4 = 20 clock cycles to do the four loads. We can see from the diagram that to get the four loads through the pipeline takes 9 clock cycles. Therefore the speedup = sequential time/actual time = 20/9 = X2.2 We can see that the MIPS process more than doubles the efficiency of the system. |
|

Custom Search