Image formation - reflection

If we give each object in a program its own light intensity then we can write this as

I = k_i

where I is the intensity of the observed light, and k_i is the i^th object's intrinsic emission intensity.

This is not going to produce very realistic graphics. Each each object wiould have an independent uniform colour. We could not make out any detail - only its silhouette. This could also lead to an unrealistic discrepancy in light intensity of neighbouring objects.

A better idea is to have all objects react to a common light source. This is what happens in reality. The light source bathes the object in light, some of that light is reflected or scattered and that is what enters the eye.

The observed light intensity (the light that goes into the eye) is therefore a function of:

the light source's intensity
the object's reflective properties (texture and colour - these will affect how much of the light is reflected)

The diagram below shows how the object's properties can affect how we percieve its colour.

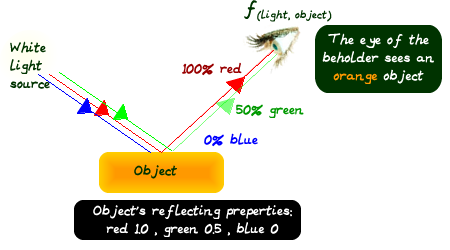
There are three types of reflected light that we need to consider when making graphic images.

Ambient

I_a = L_ak_a where

L_a is the intensity of the ambient light

k_a is the object's ambient reflection coefficient.

Ambient light is diffuse and non-directional. It illuminates all objects in the same way, no matter where they are.

You can think of it as light that has been reflected by all objects a great many times - a sort of background, non-directional light.

It hits all objects with the same intensity in all directions and reflects off all objects of the same properties in the same way no matter where they are positioned.

Diffuse

I_d = L_dk_d cos θ

where

L_d is the diffuse intensity of the point light source

k_d is the object's diffuse reflection coefficient (between 0 and 1)

θ is the angle of incidence

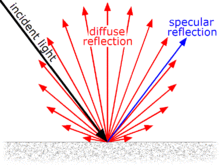Diffuse reflection is the reflection of light from a surface such that an incident ray is split into many rays of smaller intensity that spread out from the incidence point - reflecting at many angles rather than at an angle equal to the angle of incidence. Put simply, the light fans out from the incidence point!

An illuminated 'ideal diffuse reflecting surface' will have equal luminance from all directions in the hemisphere surrounding the surface. This is called Lambertian reflectance.

Specular

I_s = L_sk_s cos αⁿ

= L_sk_s(r.v)ⁿ

Specular reflection is described by the law of reflection, which states that the direction of incoming light (the incident ray), and the direction of outgoing light reflected (the reflected ray) make the same angle with respect to the surface normal, thus the angle of incidence equals the angle of reflection.

This will be what you learnt in physics at school.

Light illuminating your object will be a combination of all three types: