Binary Code
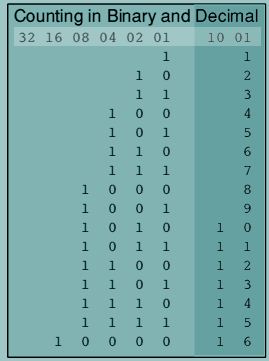
The number 11111111 in binary is 255 in decimal. Therefore using eight bits you can make 256 different binary numbers (if you include 00000000). That means that an '8-bit register' can have 256 different 'states'. Binary is a number system with a base of 2. That means only two symbols are used to express numbers in binary (bi means two): 0 and 1. We are used to a number system with a base 10 - in our decimal system (deci meaning ten) ten symbols are used to represent numbers - 0 1 2 3 4 5 6 7 8 9 Counting in binary is similar to counting in any other number system. Beginning with a single digit, counting proceeds through each symbol, in increasing order. When the symbols for the first digit are exhausted, the next-higher digit (to the left) is incremented, and counting starts over at 0. In decimal, counting proceeds like so:
After a digit reaches 9, an increment resets it to 0 but also causes an increment of the next digit to the left. In binary, counting is the same except that only the two symbols 0 and 1 are used. Thus after a digit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next digit to the left:
Binary Integer Representations
Useful links: |
|
Custom Search
The computer speaks 'binary'. Binary is a code with only two states - high and low - 1 or 0 - 'on' or 'off' - it is ideal for communication within any electrical system. Each '1' or '0' in the code is called a binary digit or '
